作者，Sean Li 。原文《10 Mind Blowing Mathematical Equations》

　　翻译，小米，哆嗒数学网翻译组成员。

　　很多时候，人们认为数学公式只是为了记忆来应付考试的。但有些时候，数学公式的价值却远超于此——它们本身就是艺术品，为纯粹的享受而生。今天我就收集了以此为目的的10个最惊人、眩目和疯狂的数学公式。这些方程应该能向任何人说明，数学不仅仅只是公式的记忆。

　　1. 欧拉恒等式

　　

　　这是一个非常著名的恒等式。它给出了3个看似随机的量之间的联系：π、e和-1的平方根。许多人认为这是数学中最漂亮的公式。

　　一个更一般的公式是e^(ix) =cosx+isinx (a^b表示a的b次方，下同)。当x=π，cosx取值为-1，而isinx取值为0。由-1+1=0，我们得到了欧拉恒等式。

　　2. 欧拉乘积公式

　　

　　等式左边的符号是无穷求和，而右边的符号则是无穷乘积。这个公式也是欧拉首先发现的。它联系了出现在等式左边的自然数(如n=1，2，3，4，5等等)与出现在等式右边的素数(如p=2，3，5，7，11等等)。而且我们可以选取s为任意大于1的数，并保证等式成立。

　　欧拉乘积公式的左边是黎曼ζ函数最常见的一种表示形式。

　　3. 高斯积分

　　

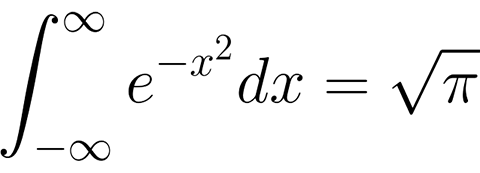
　　函数e^(-x?2;)本身在积分中是很难对付的。可是当我们对它在整个实数轴上积分，也就是说从负 无穷到正无穷时，我们却得到了一个十分干净的答案。至于为什么曲线下面的面积是π的平方根，这可不是一眼就能看出来的。

　　由于这个公式代表了正态分布，它在统计中也十分重要。

　　4. 连续统的基数

　　

　　上面的公式说明了实数集的基数与自然数全体子集的基数相同。这首先是被集合论的建立者康托尔证明的。值得注意的是，这也说明了连续统是不可数，因为2^N > N。

　　一个相关的假设是连续统假设。这个假设是说，在N和R之间不存在其它的基数。有趣的是，这个假设有一个奇怪的性质：它既不能被证明也不能被证伪。

　　5. 阶乘函数的解析延拓

　　

　　阶乘函数通常被定义为n!=n(n-1)(n-2)……1。但是这个定义只对n是正整数时有效，而上面积分方程则对分数和小数也有效，而且还可以用于负数、复数等等……

　　同样的积分式中我们把n换成n-1就定义了伽马函数。

　　6. 勾股定理

　　

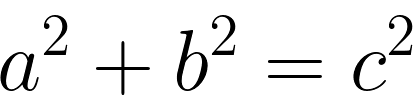
　　勾股定理恐怕是这个清单中最熟悉的公式了。它给出了直角三角形三边的联系，其中a和b是直角边长，而c是斜边长。这个公式还将三角形和正方形联系了起来。

　　7. 斐波那契数列的通项

　　

　　这里，注意到φ这个数字是黄金分割比例。很多人可能听说过斐波那契数列(0，1，1，2，3，5，8，13，21，34，55…，数列中每一项是前两项的和)，却很少人知道有一个公式能够计算出任意某一项斐波那契数：这就是上面我们给出的公式，公式里面F(n)代表第n个斐波那契数。也就是说，为了得到第100个斐波那契数，你不需要去计算前99个，而只需要把100代入公式。

　　值得注意的是，即便在计算过程中出现了许多根号和除法，最后的答案总是一个精确的正整数。

　　8. 巴塞尔问题

　　

　　这个公式告诉我们，如果你取所有完全平方数并将它们的倒数和相加，你将会得到\pi^2/6。这是欧拉首先证明的。注意到这个式子只是在前面的第二个方程(欧拉乘积公式)中令s=2。后者是黎曼ζ方程，因此我们可以说ζ(2)的值是π?2;/6。

　　9. 调和级数

　　

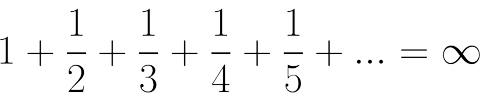
　　这个公式有点反直觉，因为它告诉我们，如果你把一些不断变小的数(最终趋向0)加起来，最后将会得到无穷。可是如果你是取它们的平方，和却是一个有限的值(答案是π?2;/6)。如果仔细观察调和级数，你会发现它正是ζ(1)。

　　10. 素数计数公式的显式表达

　　

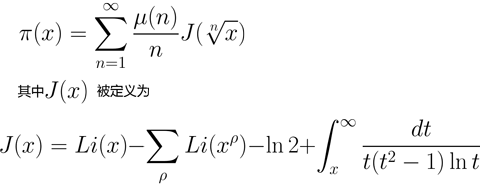
　　这个方程的重要性体现在：

　　素数是那些除了1和它本身以外没有其它因子的数。小于100的素数有2，3，5，7，11，13，17，19，23，29，31，37，41，43，47，53，59，61，67，71，73，79，83，89，97 。 由此可知，素数的出现没有显然的规律：对于一串连续正整数，有时候你会找到许多素数，有时候你会一个也找不到。找到很多或一个找不到似乎是完全随机的。

　　很长时间以来，数学家都在尝试给出素数分布的规律。上面的公式正是不大于一个给定数素数个数的显式表达。

　　以下是各个符号的意义：

　　π(x): 素数计数函数。它给出了不大于一个给定数的素数个数。例如，π(6)=3，因为有3个素数不大于6：2，3，5。

　　μ(n): 莫比乌斯函数。它依据n的质因数分解而取值为0， -1或1。

　　Li(x): 对数积分函数。它被定义为函数1/lnt从2到x的积分。

　　ρ: 黎曼ζ函数的任意非平凡零点。

　　令人吃惊的是，整个公式的结果总是一个精确的正整数!这说明，给定一个实数，我们可以把它代入公式并得到不大于它的素数个数。存在着这样一个公式的事实说明，素数的分布存在某些规律，只是我们现在还不能理解罢了。